ほとんどの人が「平均値」にすぐだまされる
先日、とあるデータをいただいた。まずはこのデータをご覧ください。
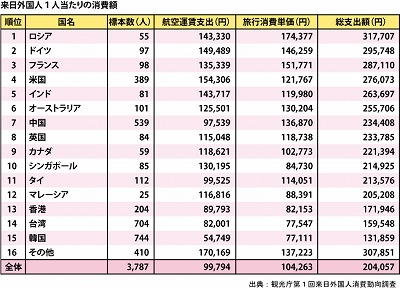
さて、この表を見て「おーなるほど、やはり欧米人が日本でカネを落としてるなぁ。」「彼らをこれからターゲットにしないとなぁ」とか思います?
このデータの解析方法の詳細はわかりませんが、表を読み取るとおそらく標本数の人数から金額を聞きだして算出したということかと推測できます。
本来はこれらの平均値の差は、t検定という手法でこれらの平均値の差に意味があるのかどうかを探ることができます。「差がある」と判断されれば、各市場に特徴があり、異なるマーケティング手法が必要になるという判断をすることができます。
その辺はある程度つかんではおりますが…。この手のデータ(平均値)を見るとき、まず考えてほしいのは平均値だけで物事を判断してはいけないことです。
【ポイントその1 標準偏差を意識する】
平均をとるときに重要なのは、「標準偏差(σ(シグマ))」という数値が裏に隠れていることです。
例として下の5年1組・5年2組各クラス5人のテスト点数結果を見てみましょう。たとえば、5人のテストの点数が以下の場合
| 5年1組 | 48点 | 49点 | 50点 | 51点 | 52点 |
| 5年2組 | 30点 | 40点 | 50点 | 60点 | 70点 |
1組も2組も、平均点はいずれも 50点ですね。しかし実は、標準偏差が異なります。
標準偏差とは「数値のバラツキ具合」です。(あまり意味がないので計算式は省略)
5年1組の標準偏差(σ(シグマ))は1.41
5年2組の標準偏差(σ(シグマ))は14.14 です。
数字がでかければ、めっちゃバラツイているわけ。標準偏差(σ(シグマ))を2倍した数の前後の数値に全体の数値の95%が存在します。下のグラフを正規分布とよび、真ん中の0のところが平均点 そこから右が平均より上、左が平均より下を意味しています。必ず釣り鐘のようなグラフを描くことが数学的に証明されています
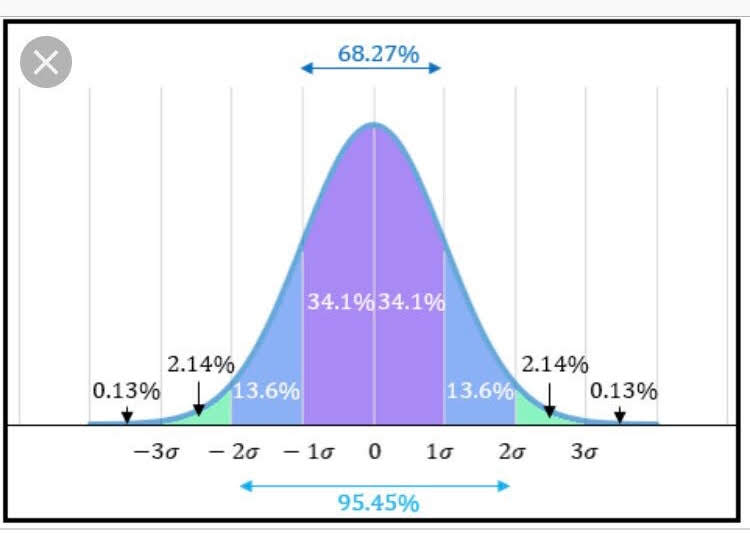
先ほどの5年1組と5年2組の例に戻ると、標準偏差をチェックすると各クラスのメンバーの実力に大きな違いがあることに気づきます。
○5年1組の場合は
1.41×2=2.82 平均50点±2.82= 47.18点~52.82点
○5年2組の場合ですと
14.14×2=28.28 平均50点±28.28= 21.72点~78.28点
この95%の数値のバラツキ度を見ると、学力が高い子と低い子が2組の方に混在しているという、1組と2組で特徴が異なっていることがわかります。
さて。今回のデータを見た場合、標準偏差が不明です。となると、国別の標準偏差を持ってきて想像するしかありません。国別の標準偏差とはなにか?それはジニ係数です。ジニ係数は、所得格差をあらわす指数です。
係数そのものを標準偏差として使うことはできませんが係数の値を確認して、皆が平均値に近いカネを使っているのかそれとも人によってバラつきがあるのか?を推測できます。ちなみに2010年現在の日韓中ではジニ係数がもっとも低いのは韓国。韓国の平均値は僕も結構納得できていますが、上位国はかえってバラつきが高いと推測しています。
【ポイント2 分母・分子を見極める】
今回のデータのように平均値しかない数値を見た場合は、自分なりに仮説を立てて読み取らなければなりません。
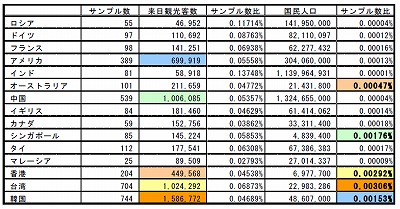
今回の調査対象については、来日観光客数と人口という大きな母数を知ることができます。そこから傾向を読み取ることしかないわけです。想像に難くないですが、表の上の国の方々はさほど来日していない。となると考えられるのは
「一部の金持ちだけが来ている」
「めったに来ないので、たくさん金を使った」
ということです。単価で13位~15位になっている3地域は、来日数ではトップレベルの地域です。
つまり、国別の単価を出すことは非常に重要ですが「順位に意味がない」ことが想像できると思います。
政府や自治体が出す、この手の単価データで見落としてはいけないことは「延べ人数」でしかないことです。グロスデータってことですね。来日者数が多い地域に関しては「リピートする顧客」というネットを見逃さないようにしなければなりません。
この記事を読む人が、読んでいるほかのブログ
解説|結論と結果の違い 美味い天ぷら屋を、食べずに判断する(1)
